Automorf formák, szinapszisok, gombák
A Sajátformák becslése aritmetikus sokaságokon című pályázat az automorf formák jobb megértésére irányul. De mik azok az automorf formák? A kutatócsoportot irányító Harcos Gergely (MTA Rényi Alfréd Matematikai Kutatóintézet munkatársa) szerint ezek gazdag szimmetriával rendelkező harmonikus hullámok, amelyek mély kapcsolatot teremtenek a matematika több nagy területe: a számelmélet, csoportelmélet, geometria, analízis, matematikai fizika között. Hasonlóan bújnak meg a számok mindenki számára látható világa mögött, ahogyan a természet makroszkopikus folyamatai mögött megbújnak az elemi részecskék és az őket leíró hullámfüggvények.
Az automorf formák fogalmát és hasznosságát az egyik legrégebbi számelméleti tételen keresztül érzékeltette Harcos Gergely.
 Automorf forma: aritmetikus szimmetriákkal rendelkező harmonikus hullám
Automorf forma: aritmetikus szimmetriákkal rendelkező harmonikus hullámMár az i. sz. 3. században élt nagy görög matematikus, Diophantosz is utalásokat tesz az Arithmetica című könyvében arra, hogy minden pozitív egész szám előáll négy négyzetszám összegeként (pl. 2016 = 442 + 82 + 42 + 02). Ez a tény elsőre meglepő, hiszen a négyzetszámok sorozata folyamatosan ritkul. A bizonyítás sem nyilvánvaló, és csak Joseph-Louis Lagrange – Olaszországban született francia matematikus – találta meg 1770-ben. Carl Gustav Jacobi német matematikus 1834-ben mélyebben megértette a problémát. Őt nemcsak az érdekelte, hogy egy adott n szám előáll-e négy egész szám négyzetének összegeként, hanem az is, hogy hány ilyen előállítás van, figyelembe véve az előjeleket és a tagok sorrendjét is. Például, ha n = 20, akkor összesen 144 előállítás van: négy előállítást ad a 20 = (±4)2 + (±2)2 + 02 + 02, amiből 48 előállítást kapunk a tagok sorrendjének variálásával, illetve 16 előállítást ad a 20 = (±3)2 + (±3)2 + (±1)2 + (±1)2, amiből 96 előállítást kapunk a tagok sorrendjének variálásával. Jacobi azt fedezte fel, majd bizonyította is, hogy az előállítások száma nem más, mint 8-szor a 4-gyel nem osztható osztók összege. Az előbbi példánkban n = 20, aminek a 4-gyel nem osztható osztói az 1, 2, 5, 10, tehát Jacobi képlete szerint az előállítások száma 8 · (1 + 2 + 5 + 10) = 144. Stimmel. Mivel minden pozitív egész számnak van 4-gyel nem osztható osztója (nevezetesen az 1), ezért Jacobi tételéből azonnal következik Lagrange tétele.
Jacobi nagy ötlete az volt, hogy az egyes előállításszámokat nem külön-külön, hanem együtt vizsgálta. Konkrétan a keresett előállításszámokat elkódolta egyetlen függvénnyé, ami a hiperbolikus sík minden pontjához hozzárendel egy mennyiséget (egy komplex számot). Kiderült, hogy az egyes függvényértékek nem függetlenek egymástól, hanem bizonyos szabályok szerint ismétlődnek. Jacobi függvénye egy aritmetikus szimmetriákkal rendelkező harmonikus hullám, röviden automorf forma. Azóta kiderült, hogy az automorf formák univerzális objektumok, amelyek a számelmélet (és csoportelmélet, geometria, analízis, matematikai fizika) nagy kérdéseiben lépten-nyomon előjönnek. A hatékonyságuk rejtélyes, de tagadhatatlan. Hogy egy konkrét példát említsünk a közelmúltból: Pierre de Fermat francia matematikus (polgári foglalkozására nézve jogász) 1637-es híres sejtését 1994-ben Andrew Wiles angol matematikus automorf formák segítségével bizonyította. Ha a Fermat-sejtésre lenne ellenpélda, akkor abból Wiles tétele szerint származtatható lenne egy olyan automorf forma, amely túl sok szimmetriával rendelkezne, és ezért nem létezhet. „Pályázatunkban azt tűztük ki célul, hogy általános (például magasabb dimenziós hiperbolikus terek feletti) automorf formákat vizsgáljunk analitikus szempontból: például mekkorák és milyen gyakoriak a hullámhegyek. A módszer is érdekes: ahogy Jacobi az előállításszámokat együttesen vizsgálta egyetlen automorf formával, úgy a kutatócsoport több automorf formát vizsgál együttesen egyetlen diofantikus keretrendszerrel” – tájékoztatott Harcos Gergely. Olyan ez, mintha a fizikában egy makroszkopikus folyamatot kvantumfizikai tényekkel magyaráznánk, de az utóbbi tényekre egy másik makroszkopikus folyamat segítségével következtetnénk.
Az idegtudomány egyik alapvető kérdése, hogy miként képes az idegi sejthálózat életünk eseményeit emlékekként rögzíteni és tárolni. Az MTA Kísérleti Orvostudományi Kutatóintézet Lendület Idegi Jelátviteli Kutatócsoportja Makara Judit vezetésével az agy kivételes információfeldolgozási és tárolási képességét megalapozó sejt- és hálózati szintű mechanizmusok megértésére törekszik. Szinapto-dendritikus jelfeldolgozás szerepe a hippokampális információkódolásban című kutatásuk során azt is vizsgálják, miként kódolja agyunk a külvilágból érkező információkat. A csoportot vezető Makara Judit szerint a tanulási folyamatokban kritikusan fontos agyterületen, a hippokampuszban a külvilágból érkező információk kódolása térben elszórtan elhelyezkedő idegsejtcsoportok összehangolt aktivitása révén történik. Az információkódoló sejtcsoportok kialakulásának sejtszintű mechanizmusai azonban kevéssé ismertek.
Korábbi, rágcsálók agyszeletében végzett kutatásaik feltártak olyan alapvető szinaptikus jelintegráló mechanizmusokat, melyek elősegítik a hippokampusz piramissejtjeinek információfogadó nyúlványaiban, a dendritekben lokális aktív feszültségjelek, úgynevezett dendritikus spike-ok kialakulását erőteljes egyidejű szinaptikus bemenet hatására. Ezek a dendritikus mechanizmusok lehetővé tehetik az idegsejt számára a hálózati aktivitás által produkált, összetett szinaptikus mintázatok érzékelését, amellyel elősegíthetik a kódoló sejtcsoportok kiválasztódását.
Érdekes módon friss irodalmi adatok szerint a funkcionálisan összetartozó szinapszisok gyakran egymáshoz igen közel, kis csoportokban (klaszterekben) helyezkednek el a dendriteken. Ez arra utal, hogy a spike küszöbét el nem érő helyi szinapto-dendritikus interakciók is hozzájárulhatnak az idegsejtek működéséhez; ezekről azonban viszonylag keveset tudunk. A munkacsoport hipotézise szerint a kódoló idegsejtek kiválasztódását mind a szinaptikus tulajdonságok, mind a korrelált szinaptikus jelek lokális dendritikus feldolgozásának dinamikus változásai elősegítik. Kutatási programjukban arra keresik a választ, hogy milyen változások következnek be a szinaptikus és dendritikus tulajdonságokban tanulási feladatot végző állatban az információkódoló sejtcsoportok kialakulása során, továbbá, hogy milyen helyi kölcsönhatások alakulhatnak ki a funkcionálisan hasonló szinapszisok között, és ezek hogyan befolyásolják a szinapszisok hosszú távú működését. E sejtszintű idegi mechanizmusok feltárása érdekében a már eddig is használt élvonalbeli in vitro módszereket (patch-clamp elvezetés, kétfoton-mikroszkópos képalkotó és stimuláló technikák akut agyszeletben) új módszerekkel, élő állatban végzett in vivo (képalkotó, patch-clamp és optogenetikai) kísérletekkel ötvözik majd.
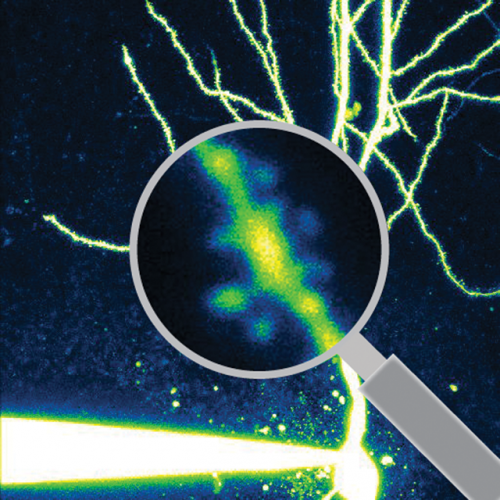 Egy hippokampális piramissejt dendritjei és dendrittüskéi a nagyító alatt
Egy hippokampális piramissejt dendritjei és dendrittüskéi a nagyító alattA jelenlegi pályázatban fontos szerepet kap az új technikák beállítása és az újabb ERC-pályázat beadásához szükséges előkísérletek elvégzése. „Természetesen hosszabb távon az a cél, hogy ezeknek a kérdéseknek a megválaszolásával kutatásunk közvetlenül hozzájáruljon a tanulás és emléktárolás sejt- és hálózati szintű alapjának, az idegrendszer óriási komputációs kapacitásának a megértéséhez. A neuronhálózat funkcionális szerveződését és élettani működését meghatározó alapvető elvek megismerése pedig remélhetőleg új stratégiai utakat nyithat meg az idegrendszer kóros működéséből eredő idegi zavarok kezelésében” – magyarázza Makara Judit.
A soksejtűség kialakulásához vezető evolúciós lépések megértéséhez járul hozzá Nagy G. László vezetésével az MTA Szegedi Biológiai Kutatóközpont Biokémiai Intézet Lendület Gomba Genomika és Evolúció Csoportjának projektje. A soksejtű gombák evolúciós eredetének vizsgálata filogenetikai és genomikai módszerekkel című kutatás a biológia új módszertani, elsősorban bioinformatikai és genomikai eredményeire támaszkodik.
„A soksejtűség kialakulása az evolúció egyik olyan lépése volt, amely nélkül a földi élet a mai formájában nem alakulhatott volna ki. Így a ma élő állat- és növényfajok – beleértve az embert – megjelenésének is egyik sarokköve volt. Azt szokták mondani, ez a biológia egyik nagy kérdése. A soksejtűség megjelenése számos előnnyel járt: az egysejtű mikrobákhoz képest a soksejtű élőlények új típusú élőhelyeket tudtak benépesíteni, nagyobb volt a testméretük, így kevésbé voltak kiszolgáltatva a ragadozóknak. A sejtek közötti munkamegosztás megjelenése pedig különböző sejttípusok, majd szövetek és szervek kialakulásához vezetett” – avat a részletekbe a szegedi kutató.
Gombák esetében a soksejtű növekedésnek közvetlen gazdasági vonatkozásai is vannak; azok a gombák, melyek képesek váltani egysejtű élesztőszerű és soksejtű fonalas formák között, sokkal gyakrabban tudnak betegségeket okozni mind állatokban, mind növényekben, mint azok a fajok, amelyek vagy csak egysejtű, vagy csak soksejtű formában tudnak létezni. Ezért a gombák soksejtűségének megértése alkalmazott, egészségügyi vonatkozásokkal is bír.
Azért éppen a gombák genomjának megismerésére vállalkoznak Szegeden, mert a gombák nagyon jó modellorganizmusok. Gombák esetében a komplex soksejtűség – amelyen háromdimenziós soksejtű struktúrákat értünk – két lépésben alakult ki: az egysejtű ősökből először egyszerű fonalakból (micélium) álló telepek jelentek meg, ide tartozik a ma ismert gombák jelentős része, az úgynevezett fonalasgombák. Ezután néhány fonalasgomba-csoportnál megjelentek termőtestek, amelyeket klasszikus értelemben ’gomba’-ként ismerünk. A termőtestek ivaros szaporodással képződnek, és könnyen indukálhatóak laboratóriumi körülmények között. Tehát míg gombáknál valós időben vizsgálhatják a komplex soksejtűség kialakulását, addig állatoknál és növényeknél ennek a több százmillió éves evolúciós eseménynek a kutatása korlátokba ütközik. Ennek az átmenetnek a tanulmányozására vállalkozott a szegedi kutatócsoport a legkorszerűbb összehasonlító genomikai és bioinformatikai módszerek segítségével. Az alapvető kérdés, hogy milyen gének és gének expresszióját szabályozó genomi részek játszanak szerepet a soksejtűség kialakulásában, ezek evolúciósan honnan erednek, és hogy hatnak kölcsönösen egymásra a soksejtű szervezetek fejlődése során?
A kutatás egyik sarokköve hatékony bioinformatikai eljárások kifejlesztése. Az új generációs genomszekvenálási technológiáknak köszönhetően rövid idő alatt hatalmas adatmennyiséget tudnak generálni, ennek analízise, de tárolása és kezelése is óriási kihívás. Ebben az értelemben a Big Data jelenség különösen érvényes a genomikában – az adatgenerálás sebessége ma messze meghaladja az analitikai kapacitásokat. A kihívást részben az jelenti, hogy ki tud hatékonyabb, az adott kérdéshez jobban illeszkedő analitikai stratégiát fejleszteni. Ebből adódóan a biológusok számára is felértékelődnek a programozási és számítógépes ismeretek, hiszen a kutatás meghatározó lépései számítógépen történnek. Ráadásul minden analízist a fajok filogenetikai (rokoni) kapcsolatainak figyelembevételével kell elvégezni, és ez szintén új terület, a filogenomika, számos kihívással és megoldandó kérdéssel.
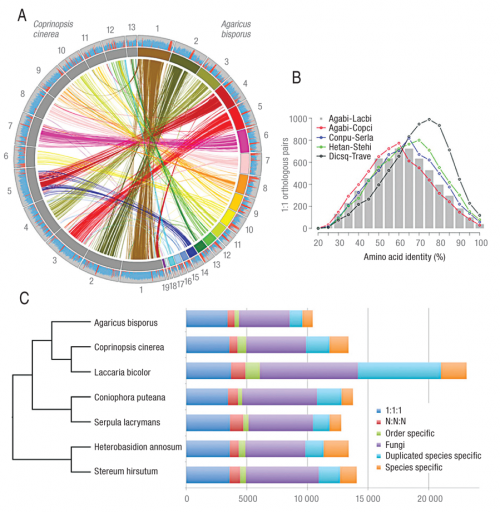 Az összehasonlító genomikai módszerek betekintést engednek az élőlényeket kódoló teljes genetikai kódba, ennek megfejtése azonban komoly bioinformatikai kihívás még a mai szuperszámítógépek számára is
Az összehasonlító genomikai módszerek betekintést engednek az élőlényeket kódoló teljes genetikai kódba, ennek megfejtése azonban komoly bioinformatikai kihívás még a mai szuperszámítógépek számára is„Abban a szerencsés helyzetben vagyunk, hogy rengeteg saját és mások által szekvenált, de publikálatlan genomszekvenciához férünk hozzá, így minden, a modellorganizmusokban megfigyelt jelenséget egy sok fajt felölelő összehasonlító kontextusban is vizsgálhatunk. Ez a soksejtűséghez vezető evolúciós események megértése szempontjából rendkívül fontos, és a projektet nagyban fogja segíteni” – tudtuk meg Nagy G. Lászlótól.
A kutatás egyik alapvető célja előkísérletek elvégzése és előzetes eredmények generálása az Európai Kutatási Tanács pályázatához. Ezenkívül természetesen cél a soksejtűséghez vezető genomi folyamatok és általánosságban az evolúció törvényszerűségeinek feltárása, amelyek más kutatásokban is felhasználhatók.•























